05_tttt_measurement.md 9.6 KB
title: Measurement of the $t\bar{t}t\bar{t}$ Cross Section at 13 TeV ...
Featuring high jet multiplicity and up to four energetic leptons, four top quark production is among the most spectacular SM processes that can occur at the LHC. It is also a rare process with a production cross section calculated to be $12.0^{+2.2}_{-2.5}\mathrm{fb}$ at Next-to-Leading Order (NLO) at 13 TeV center of mass energy[@Frederix2018]. Previous searches at ATLAS and CMS have set limits on the cross section of XXX and YYY. The goal of this analysis is to improve upon previous results by analyzing a larger dataset and utilizing improved analysis methods.
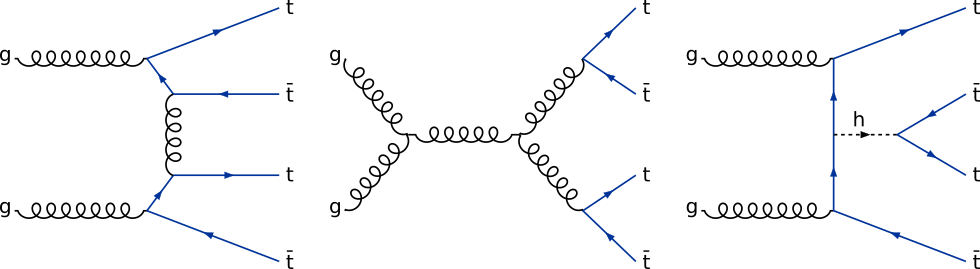
The production of four top quarks is possible through a variety of SM diagrams. [@fig:ft_prod_feyn] shows a few of these diagrams. The purely gluon mediated diagrams contribute roughly 90% of the total cross section, with electroweak and Higgs mediated diagrams contributing the remainder.
Top quarks are unique among quarks in that they are heavy enough at 173 GeV to decay weakly. This results in them having the extremely short lifetime of around $5\times10^{-25}$s. This is much shorter than the timescale for hadronization (XXX) so they decay almost exclusively to a W boson and a down type quark. Of these decays, the $W+b$ channel is heavily favored due to $|V_{tb}|$ being very close to unity. Therefore, the final state particles of an event with top quarks are determined by the decay mode of the child W boson. Approximately 67% of W bosons decay to lighter flavor (ie not top) quark antiquark pairs, while the rest will decay to $e$, $\mu$, and $\tau$ leptons in approximately equal probability. Electrons and muons can be observed directly while tauons will themselves decay to either $e/\mu$, or hadrons.
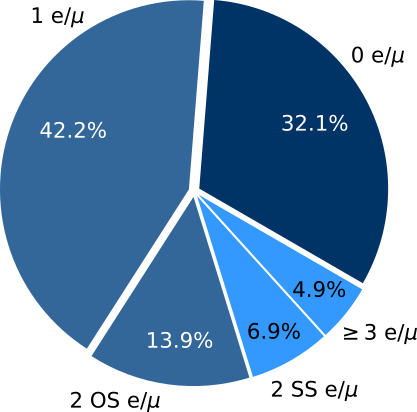
For four top quarks, the final states are conventionally defined in terms of the number and relative charges of $e/\mu$ leptons. This is summarized in [@fig:ft_final_states] with the coloring indicating the three analysis categories: fully hadronic, single lepton or opposite sign dilepton, and same sign dilepton or 3 or more leptons, where lepton here and henceforth should be taken to mean $e/\mu$ unless otherwise noted.
Four top searches for each of these final state categories demand unique analysis strategies due to different event content and vastly different SM backgrounds. In particular, the same sign dilepton and three or more lepton category benefit from a relatively small set of SM backgrounds at the expense of a rather small overall branching ratio. This is the category that is examined in this analysis[@CMSFT2019].
The basic strategy of this analysis is to first craft a selection of events that are enriched in $t\bar{t}t\bar{t}$. This is done by cutting on relatively simple event quantities such as the number and relative sign of leptons, number of jets, number of b-tagged jets, overall hadronic activity, and missing transverse momentum. A multivariate classifier is trained on simulated events within this selection to distinguish $t\bar{t}t\bar{t}$ from background events. This MVA produces a discriminant value that tends towards one for $t\bar{t}t\bar{t}$ like events, and to zero for background like events. This discriminant is then calculated for real and simulated events and divided into several bins. Finally, a maximum likelihood fit is performed on the discriminant distribution to extract the deviation of the measured distribution from the background-only distribution. A statistically significant (and positive) deviation can then be interpreted as evidence of $t\bar{t}t\bar{t}$ production.
Datasets and Simulation
This analysis uses data collected during 2016, 2017, and 2018 with the CMS detector. This corresponds to a total integrated luminosity of 137.2 fb$^{-1}$. Events that pass the HLT are divided into roughly disjoint datasets. Of the many of these produced by CMS, this analysis uses:
- DoubleEG/EGamma: two-electron channel
- DoubleMuon: two-muon channel
- MuonEG: crossed channel targeting events with one muon and one electron
- JetHT: used to recover efficiency for dilepton+$H_T$ triggers in period 2016H (although no additional events are found in this sample.
Because the datasets are not completely disjoint, care has been taken to avoid double counting events that may occur in multiple datasets.
Monte Carlo simulation is used extensively to model background and signal processes relevant to this analysis. See chapter 4 for more details on the process of producing simulated events. Samples of simulated Standard Model process events are produced centrally by a dedicated group within the CMS collaboration [@TODO]. Because detector conditions were changed year-to-year over Run 2, this analysis uses three sets of samples, one for each year. Each year's set of samples are then re-weighted to match the integrated luminosity of that year.
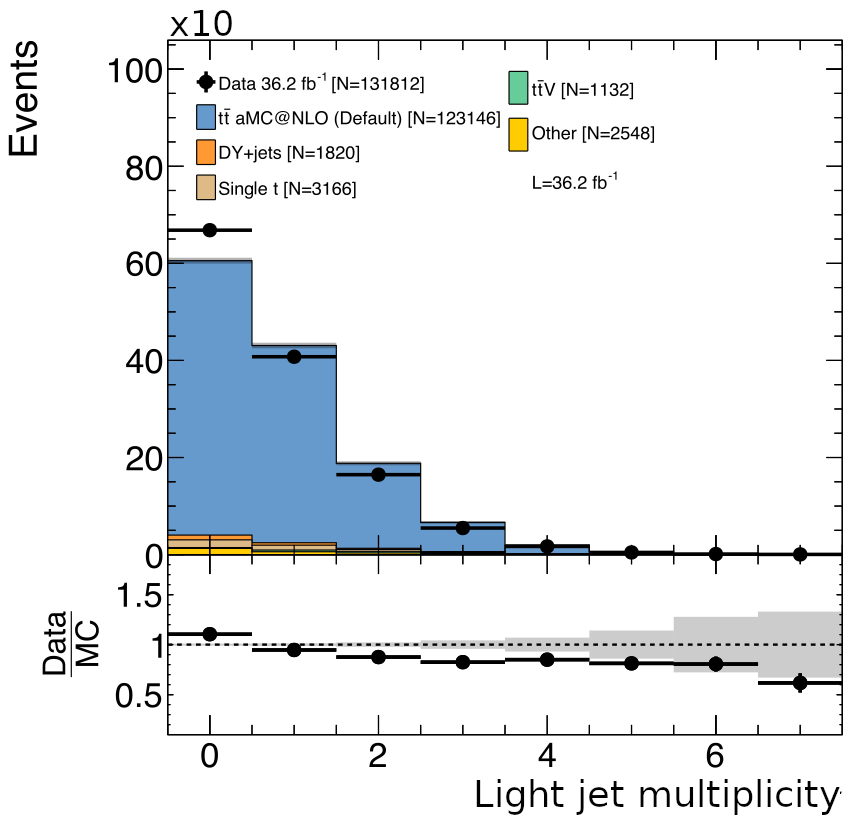
Because $N_{jet}$ is expected to be an important discriminating variable for $t\bar{t}t\bar{t}$, it is important to ensure that the spectrum of jets originating from initial state and final state radiation (ISR/FSR) is accurately modeled. This is particularly true for the major backgrounds $t\bar{t}W$ and $t\bar{t}Z$. How is this correction done? The key observation is that a mismodeling of the ISR/FSR spectra by the event generator will be very similar between $t\bar{t}+X$ and just $t\bar{t}$. So by measuring the disparity between data and MC in $t\bar{t}$, correction weights can be obtained and applied to $t\bar{t}+X$. The number of ISR/FSR jets in data is obtained by selecting dilepton $t\bar{t}$ events with exactly two identified b-jets. Any other jets are assumed to be from ISR/FSR. The results of this measurement for 2016 data and MC are shown in [@fig:isrfsr_correction].
The number of b-tagged jets is also expected to be an important discriminator for $t\bar{t}t\bar{t}$. Therefore the flavor composition of additional jets in simulation should also be matched to data. Specifically, there has been an observed difference between data and simulation in the measurement of the $t\bar{t}b\bar{b}/t\bar{t}jj$ cross-section ratio[@TODO]. To account for this, simulation is corrected to data by applying a scale factor of 1.7 to simulated events with bottom quark pairs originating from ISR/FSR gluons.
Object Definitions
This section describes the basic event constituents, or objects, that are considered in this analysis. The choice of the type and quality of these objects is motivated by the final state content of $t\bar{t}t\bar{t}$ events. These are electrons, muons, jets, b-tagged jets, and an imbalance of transverse momentum indicating the presence of neutrinos.
Electrons
Electrons are generally seen in two parts of the CMS detector: the tracker, and the electromagnetic calorimeter. One step in event reconstruction is to match tracks from the tracker with energy deposits in the ECAL. These electron candidates are then evaluated in one of a variety of schemes to determine the probability that it is from a genuine electron vs a photon, a charged hadron, or simply just an accidental match of two unrelated constituents. For this analysis, only electrons with $|\eta|<2.5$, i.e. within both the tracker and ECAL acceptance, are considered.
The particular scheme to determine the quality of an electron candidate employed for this analysis uses a multivariate discriminant built with shower-shape variables ($\sigma{i\eta i\eta}$, $\sigma{i\phi i \phi}$, cluster circularity, widths along $\eta$ and $\phi$, $R9$, H/E, $E{\mathrm{in-ES}}/E{\mathrm{raw}}$), track-cluster matching variables ($E{\mathrm{tot}}/p{\mathrm{in}}$, $E{\mathrm{ele}}/p{\mathrm{out}}$, $\Delta \eta{\mathrm{in}}$, $\Delta \eta_{\mathrm{out}}$, $\Delta \phi{\mathrm{in}}$, $1/E-1/P$), and track quality variables ($\chi^2$ of the KF and GSF tracks, the number of hits used by the KF/GSF filters, fbrem). Additional details on the construction and calibration of this discriminant can be found in [@TODO]. Find a good way to reference more detail on this. AN references internal presentations
Charge mismeasurement of leptons can result in an opposite-sign dilepton event appearing as a same-sign dilepton event. Because there are potentially large backgrounds with opposite-sign dileptons, extra steps are taken to remove events with likely charge mismeasurement. In CMS, there are three techniques for measuring electron charge [@TODO]. For the highest quality, or "tight", category of electrons used in the analysis, all three methods are required to agree. Electrons can also originate from photon conversion into electron-positron pairs. These photons will sometimes pass through one or more layers of the tracker before decaying, resulting in "missing" inner layer hits for the tracks of the child particles.
Muons
Muons are reconstructed in CMS by matching energy deposits in the muon system to tracks in the tracker. The individual quality of the tracker and muon system contributions as well as the consistency between them are used to define IDs. The muon POG defines two IDs that are used in this analysis. The
Jets
B-Jets
Missing Transverse Energy
Event Selection
Background Estimation
Systematic Uncertainties
Signal Extraction
Signal extraction can be approached in two principle ways. First,