02_standard_model.md 12 KB
title: The Standard Model of Particle Physics ...
The Standard Model of Particle Physics, henceforth Standard Model, stands as one of the most predictive and insightful scientific theories ever written. It is the culmination of a hundred years of intense theoretical exploration and experimental tests. It can sucessfully explain phenomena ranging from nuclear decay and the structure of atoms to the behavior of cosmic ray showers. Included in the theory are three fundamental forces. The first and most familiar is the electromagnetic force which is mediated by the photon and which all particles with electric charge participate. The second is the strong nuclear force. The strong force is mediated by the gluon which controls the interaction between all colored particles. It is this force that is responsible for binding quarks together into mesons and baryons, as well as binding protons and neutrons together into atomic nuclei. Finally, the weak nuclear force, which is mediated by the W and Z bosons, and is responsible for nuclear $\beta$-decay as well as more exotic processes such as interactions with the ghostly neutrino particle and the decay of the top quark.
Notably, the Standard Model is completely unable to explain why apples fall from trees or why water flows downhill since it lacks a description of the gravitational force. The current most complete theory of gravity is General Relativity. However, despite large and ongoing efforts to unite GR with the Standard Model, no resulting theories have had the necessary self-consistency and predictive power to be accepted. Luckily for those working on collider experiments, the effects of gravity are so overwhelmed by the other three fundamental forces that they can be largely ignored.
Before describing the Standard Model in more detail, however, it is important to understand how we got to where we are today[^1]. The story of particle physics has generally been that of assuming that something is a fundamental, indivisible unit of matter, whether it be molecules, atoms, or nucleons, and then discovering that that something is in fact composite. Despite this reoccuring story, however, we start with a notable exception: the electron.
[^1]: Much of this discussion loosely follows the summary given by Griffiths in [@griffiths2008].
The Electron
Back in 1897, J. J. Thompson and associates were investigating the phenomena of "Cathode Rays"[@thompson1897]. At this point the laws of Maxwell that describe electromagnetism had already been well established, as well as the fact that matter contained, as yet unidentified, charge carriers whose motion results in electric current. Indeed, earlier experiments by Jean Perrin[@perrin1895] had shown that these Cathode Rays were associated with a stream of negatively charged particles, but not not that they were one in the same. As Thompson puts it,
[Others] do not deny that electrified particles are shot off from the cathode; they deny, however, that these charged particles have any more to do with the cathode rays than a rifle-ball has with the flash when a rifle is fired.
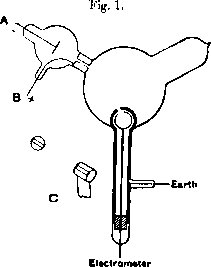
The contribution of Thompson's experiment was to show that these cathode rays were made up of negatively charged particles, or as he called them "corpuscles". The experimental setup is shown in [@fig:thompson_cathode_rays]. It consists of a cathode (A) which is simply a heated piece of metal supplied with a negative voltage with respect to earth. An anode (B) made of a metal plug with a central hole is fixed into the "neck" of the experiment and serves to draw the isotropic cathode rays into a beam and shoot it into the central bulb. The central bulb is coated with a phosphor which shows the position of the beam on the wall of the bulb. A magnetic field is then employed to deflect the beam into an electrometer shown at the bottom of the diagram.
Thompson found by tracing the path of the cathode rays using the phosphorescent coating that when the beam was bent such that it entered into the electrometer, it regestered a large jump in charge. This implied that the cathode rays and the charge carrying corpuscles were one in the same. Additional experiments by Thomson and others measured the charge-to-mass ratio of these electrons (a name coined by irish physicist George Johnstone Stoney), and found the same results whether the particle source was a heated material, an illuminated one, or from certain radioactive materials. These results lent credence to the idea that the electron was a universal component of matter, and hence the first member of the family of particles in the Standard Model was established.
The Photon
Although many early descriptions of light, chiefly those put forward by Newton[@newton], assumed it to consist of streams of particles, by the end of the 19th century diffraction and interference experiments had led to widespread acceptance of Maxwell's wave theory. Maxwell's Equations $\ref{eqn::maxwell}$ gave a unified theory for the seemingly disparate phenomena of electricity and magnetism, and gave scientists and engineers the tools to build many of the world changing inventions of the late 19th and early 20th century including mechanical power generation (dynamos), electric lighting, the telephone, radar, and so on.
\begin{align} \nabla \cdot E &= \frac{\rho}{\epsilon_0} \nonumber \ \nabla \cdot B &= 0 \nonumber \ \nabla \times E &= -\frac{\partial B}{\partial t} \nonumber \ \nabla \times B &= \mu_0 \left( J + \epsilon_0 \frac{\partial E}{\partial t} \right) \label{eqn::maxwell} \end{align}
When Maxwell's Equations are solved in the absense of charge and current (ie $\rho=J=0$), one obtains the free-field wave equations.
\begin{align} \mu_0 \epsilon_0 \frac{\partial^2 E}{\partial t^2} - \nabla^2E &= 0 \nonumber \ \mu_0 \epsilon_0 \frac{\partial^2 B}{\partial t^2} - \nabla^2B &= 0 \label{eqn::freefield} \end{align}
By dimensional analysis, we can show that the units of the quantity $\mu_0 \epsilon_0$ are an inverse speed squared. We label this speed $c$ and rewrite the above as
\begin{align} \frac{1}{c^2} \frac{\partial^2 E}{\partial t^2} - \nabla^2E &= 0 \nonumber \ \frac{1}{c^2} \frac{\partial^2 B}{\partial t^2} - \nabla^2B &= 0 \quad . \label{eqn::freefieldc} \end{align}
These are a well known type of differential equation with sinosoidal wave solutions that propogate through space at a speed $c$. During the lifetime of Maxwell, the speed of light was measured to within 0.5% of the modern value by Leon Focault and, later, by Albert Michelson using time-of-flight experiments[@michelson1878]. Somewhat earlier around 1856, Wilhelm Eduard Weber and Rudolf Kohlrausch were able the measure the quantity $\frac{1}{\sqrt{\epsilon_0\mu_0}}$ by discharging a Leyden Jar (an early type of capacitor) of known charge and measuring the resulting magnetic field[@brown2001]. What they found was a quantity matching the measured speed of light. This connection gave convincing evidence that the phenomena of light and radio waves were in fact oscillating electromagnetic fields.
Around the turn of the century then, it appeared as if physics was a more or less fully understood science. Newtonian mechanics could successfully and accurately predict the motion of the planets. Maxwell's equations fully explained electromagnetic phenomena as the interaction between electromagnetic waves and charged particles. Outside of a few soon-to-be-solved(tm) curiosities, the work of physisists was complete.
Blackbody Radiation
The blackbody spectrum describes the amount of energy in the form of electromagnetic radiation that is produced by an object in thermal equilibrium at temperature $T$ as a function of frequency. A defining feature of the blackbody spectrum is that it makes no assumptions about the microscopic details of the body itself. Stated more concretely,
For a body of any arbitrary material emitting and absorbing thermal electromagnetic radiation at every wavelength in thermodynamic equilibrium, the ratio of its emissive power to its dimensionless coefficient of absorption is equal to a universal function only of radiative wavelength and temperature. That universal function describes the perfect black-body emissive power.[@kirchhoff1860]
Kirchhoff proposed the existence of this universal function, which I will call $S_\nu(\nu, T)$ in 1860, but it would take another 40 years until this function could be convincingly derived from first principles.
The most notable failed attempt, made by Lord Rayleigh, at deriving $S_\nu$ was to imagine a "black box" as an actual 3d box containing standing electromagnetic waves. These waves have fixed, discrete wavelengths imposed by boundary conditions at the surface of the box. Each of these modes of oscillation is mathematically equivalent to a simple harmonic oscillator which, according to the equipartition theorm of classical statistical mechanics, would have an average thermal energy $k_B T$. Unfortunately, if one then attempts to calculate the total energy emission which requires summing over all frequencies, the sum diverges as one considers higher and higher frequencies. This is the so-called ultraviolet catastrophe.
The correct model was derived my Max Planck in 1900. Based upon some inspired guesswork and application of the laws of thermodynamics he hit upon the following formula.
\begin{equation} S_\nu = \frac{2\pi h}{c^2} \frac{\nu^3}{e^{h \nu / kT} - 1} \end{equation}
Where $h$, now called Planck's constant, was an adjustable parameter. The key difference between the approaches of Rayleigh and Planck was that where Rayleigh assigned all oscillation modes of the cavity an equal average energy, Planck said the energy increases with frequency as
\begin{equation} E = n h \nu \quad n \in \left{0, 1, 2, ... \right} \end{equation}
And since the different modes now have different energies, classical statistical mechanics says that the higher frequency modes are less likely to become excited. This surpresses the contribution to total energy emission from high frequency components and allows the sum over all frequencies to converge. This quantization of possible energies for the different vibrational modes was characterized by Planck as an "act of desperation" into which he was forced because "a theoretical explanation had to be found at any cost, whatever the price."[^2] However, despite his initial reservations, Planck was eventually awarded the Nobel Prize in 1919 for the "discovery of energy quanta".
[^2]: Unpublished letter my M. Planck; quoted in M. Jammer, The Conceptual Development of Quantum Mechanics, p. 22
The Photoelectric Effect
Although there had been earlier work that suggested a relationship between light and electricity (see Becquerel's studies of the photovoltaic effect [@Petrova-Koch2009]), the earliest observation of the photoelectric effect was by Heinrich Hertz in 1887[@hertz1887]. His apparatus consisted of a metal coil whose purpose was to detect the presence of electromagnetic waves (ie an antenna) with a small gap that would spark when sufficient radiation is present. To make the spark easier to see, the antenna was placed in a dark box, but Hertz found that the length across which the spark would jump shrank relative to the same experiment exposed to light. Subsequent experiments by Philipp Lenard in 1902 demonstrated that electrons emitted by an illuminated metal surface had a velocity had a velocity that increased with the frequency of the applied light, and that that light must have a sufficiently high frequency to emit any electrons at all. Most notably, a high intensity, low frequency light source would not cause any emission, which is in contradition with the wave nature of light described by Maxwell's equations.
This apparent contradiction was remedied by Albert Einstein in 1905 by describing light as arriving in discrete packets, or photons, with energy equal to frequency times a constant. Given that the electron in the material requires some amount of energy, $\phi$, to escape the material, by conservation of energy, the emitted electron will have an energy
\begin{equation} E = \hbar \nu - \phi \end{equation}
This simple equation captured both of the defining characteristics of the photoelectric effect, and, together with Planck's solution to the blackbody radiation problem, eventually led to widespread acceptance of the discrete nature of light.