LPC_stats_2017/HW3/p4.md

---

title: p4. fontsize: 8pt

geometry: margin=1cm

#!/usr/bin/env python3
""" LPC stats HW2, Problem 4
    Author: Caleb Fangmeier
    Created: Oct. 8, 2017
"""
from scipy.stats import norm, uniform, cauchy, mode
from numpy import logspace, zeros, max, min, mean, median, var
import matplotlib.pyplot as plt


distributions = {
    'uniform': lambda a, N: uniform.rvs(loc=a-0.5, scale=1, size=N),
    'gaussian': lambda a, N: norm.rvs(loc=a, scale=1, size=N),
    'cauchy': lambda a, N: cauchy.rvs(loc=a, size=N)
}

estimators = {
    'midrange': lambda xs: max(xs) - min(xs),
    'mean': lambda xs: mean(xs),
    'median': lambda xs: median(xs),
    'mode': lambda xs: mode(xs).mode[0]
}


def var_of_est(dist_name, est_name, N, a=1):
    M = 500
    estimates = zeros(M)
    for i in range(M):  # run M experiments to estimate variance
        data = distributions[dist_name](a, N)
        estimates[i] = estimators[est_name](data)
    return var(estimates)


plt.figure()
for i, distribution in enumerate(distributions):
    plt.subplot(2, 2, i+1)
    for estimator in estimators:
        Ns = logspace(1, 3, 30, dtype=int)
        vars = zeros(30)
        for i, N in enumerate(Ns):
            vars[i] = var_of_est(distribution, estimator, N)
        plt.plot(Ns, vars, label=estimator)
    plt.title(distribution)
    plt.xlabel('N')
    plt.ylabel(r'$\sigma^2$')
    plt.xscale('log')
    plt.yscale('log')
    plt.tight_layout()
    plt.legend()

plt.show()

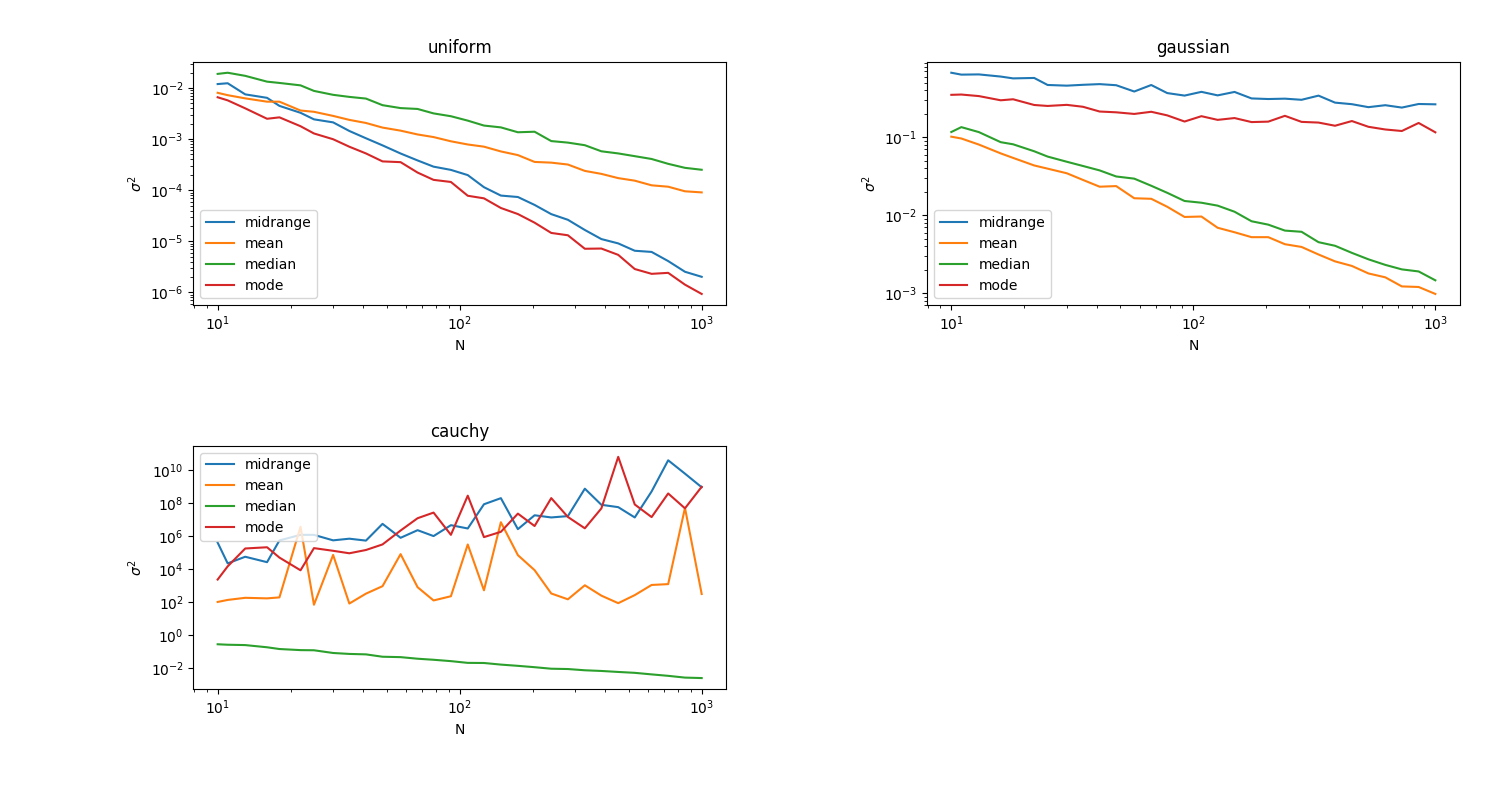
The best estimator is different for each distribution. For the uniform distribution, the midrange and mode estimators are both good, with the mode being somewhat better. However, for the Gaussian, these estimators are beat out substantially by the median and mean estimators, with the mean being the best. Finally, for the Cauchy distribution, the median estimator is clearly the best, while all of the others fall prey to the pathological nature of Cauchy and the relatively high probability of getting sample values from far out in the tails.