|
|
@@ -0,0 +1,69 @@
|
|
|
+---
|
|
|
+title: p4.
|
|
|
+fontsize: 8pt
|
|
|
+geometry: margin=1cm
|
|
|
+---
|
|
|
+
|
|
|
+```python
|
|
|
+#!/usr/bin/env python3
|
|
|
+""" LPC stats HW2, Problem 4
|
|
|
+ Author: Caleb Fangmeier
|
|
|
+ Created: Oct. 8, 2017
|
|
|
+"""
|
|
|
+from scipy.stats import norm, uniform, cauchy, mode
|
|
|
+from numpy import logspace, zeros, max, min, mean, median, var
|
|
|
+import matplotlib.pyplot as plt
|
|
|
+
|
|
|
+
|
|
|
+distributions = {
|
|
|
+ 'uniform': lambda a, N: uniform.rvs(loc=a-0.5, scale=1, size=N),
|
|
|
+ 'gaussian': lambda a, N: norm.rvs(loc=a, scale=1, size=N),
|
|
|
+ 'cauchy': lambda a, N: cauchy.rvs(loc=a, size=N)
|
|
|
+}
|
|
|
+
|
|
|
+estimators = {
|
|
|
+ 'midrange': lambda xs: max(xs) - min(xs),
|
|
|
+ 'mean': lambda xs: mean(xs),
|
|
|
+ 'median': lambda xs: median(xs),
|
|
|
+ 'mode': lambda xs: mode(xs).mode[0]
|
|
|
+}
|
|
|
+
|
|
|
+
|
|
|
+def var_of_est(dist_name, est_name, N, a=1):
|
|
|
+ M = 500
|
|
|
+ estimates = zeros(M)
|
|
|
+ for i in range(M): # run M experiments to estimate variance
|
|
|
+ data = distributions[dist_name](a, N)
|
|
|
+ estimates[i] = estimators[est_name](data)
|
|
|
+ return var(estimates)
|
|
|
+
|
|
|
+
|
|
|
+plt.figure()
|
|
|
+for i, distribution in enumerate(distributions):
|
|
|
+ plt.subplot(2, 2, i+1)
|
|
|
+ for estimator in estimators:
|
|
|
+ Ns = logspace(1, 3, 30, dtype=int)
|
|
|
+ vars = zeros(30)
|
|
|
+ for i, N in enumerate(Ns):
|
|
|
+ vars[i] = var_of_est(distribution, estimator, N)
|
|
|
+ plt.plot(Ns, vars, label=estimator)
|
|
|
+ plt.title(distribution)
|
|
|
+ plt.xlabel('N')
|
|
|
+ plt.ylabel(r'$\sigma^2$')
|
|
|
+ plt.xscale('log')
|
|
|
+ plt.yscale('log')
|
|
|
+ plt.tight_layout()
|
|
|
+ plt.legend()
|
|
|
+
|
|
|
+plt.show()
|
|
|
+```
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
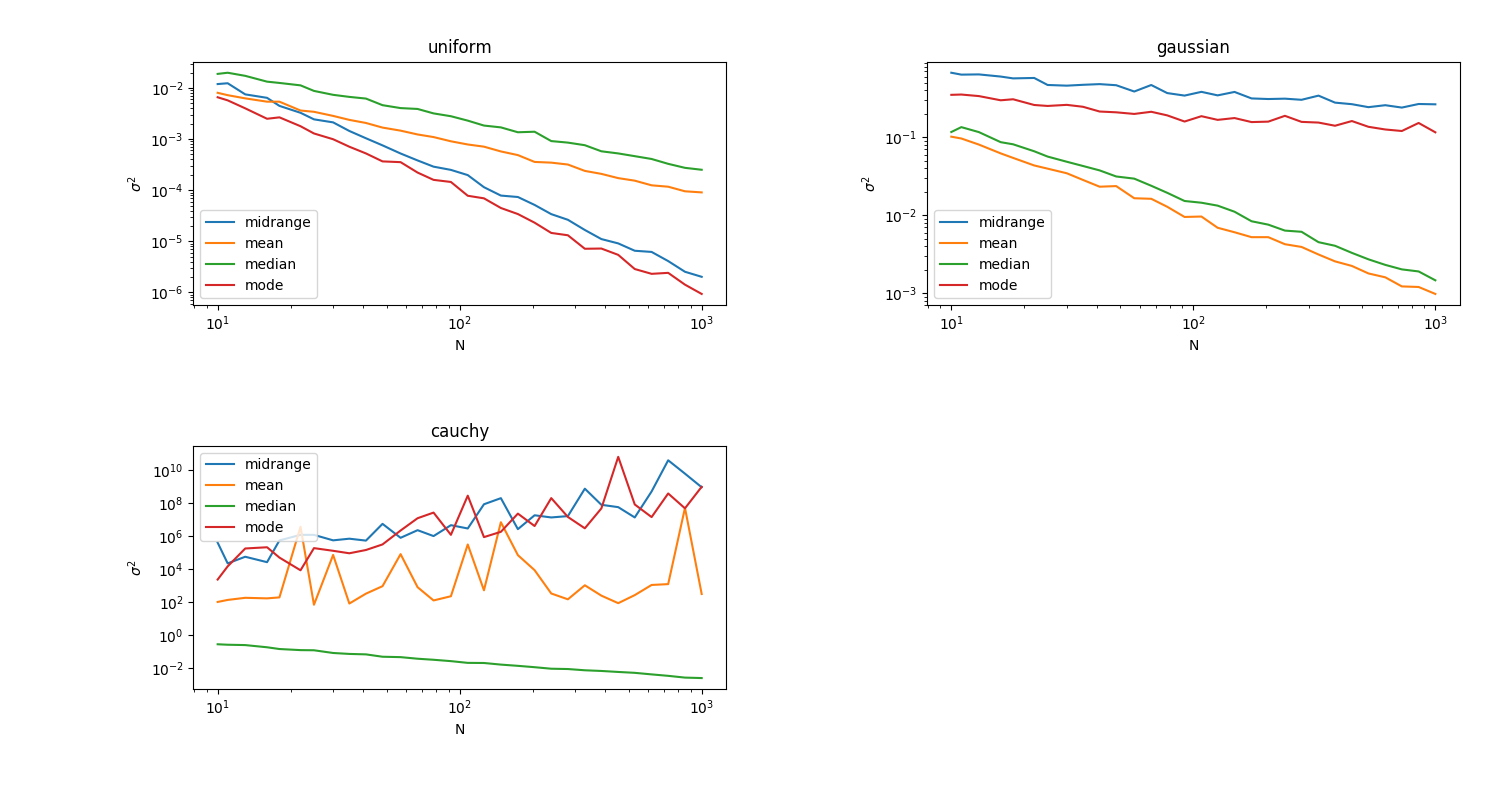
+The best estimator is different for each distribution. For the uniform
|
|
|
+distribution, the midrange and mode estimators are both good, with the mode
|
|
|
+being somewhat better. However, for the Gaussian, these estimators are beat out
|
|
|
+substantially by the median and mean estimators, with the mean being the best.
|
|
|
+Finally, for the Cauchy distribution, the median estimator is clearly the best,
|
|
|
+while all of the others fall prey to the pathological nature of Cauchy and the
|
|
|
+relatively high probability of getting sample values from far out in the tails.
|